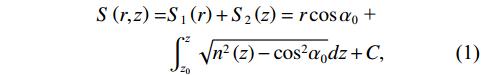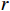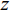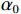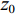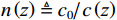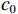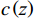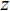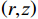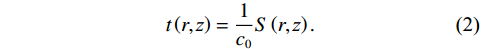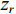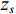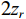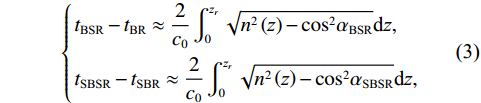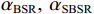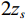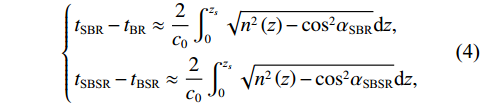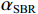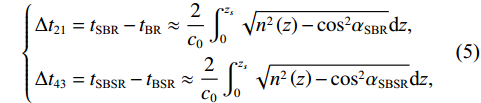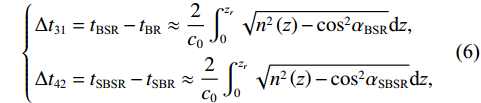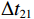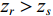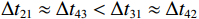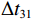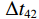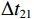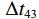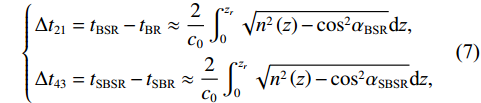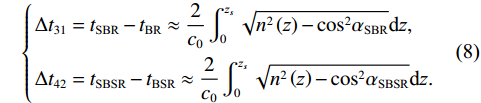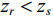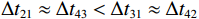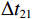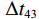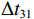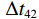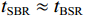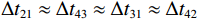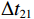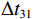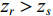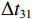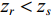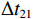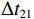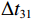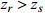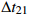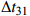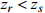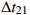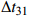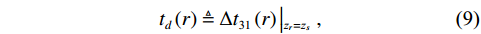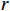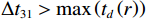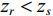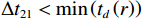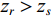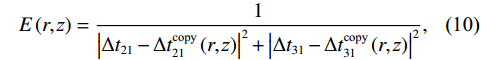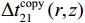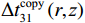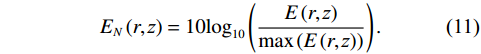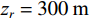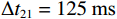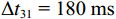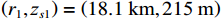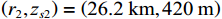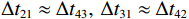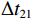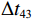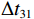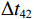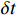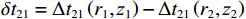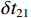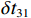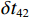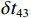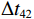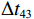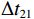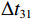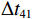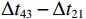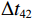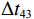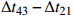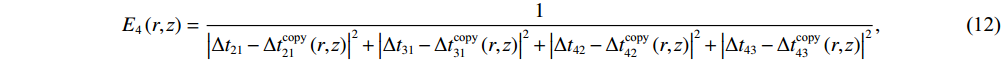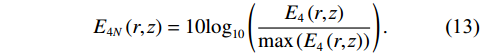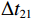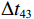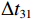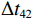A range and depth estimation method using the time delay structure of bottom reflection in deep sea bottom bounce area
-
摘要:
针对收发深度关系未知时利用时延差进行距离深度估计可能会出现伪源的问题, 提出了一种利用4个时延差直接进行距离深度估计的方法。该方法通过分析4条多径间4个时延差的关系, 利用伪源与真实位置间同种时延差的差异, 构造模糊平面进行定位, 无需判断收发深度关系即可排除伪源, 且在单水听器上即可实现。仿真实验与误差分析验证了该方法的有效性, 海试结果表明, 该方法在两个不同深度的单水听器上均成功实现了对11.0~16.5 km目标的距离深度估计, 距离和深度的均方根误差分别小于1.1 km和54 m。
Abstract:When the depth relationship between source and receiver is unknown, using the time delay differences for distance and depth estimation may result in a pseudo source. To address the issue, a method for directly estimating distance and depth using four time delay differences has been proposed. This method analyzes the relationship of four time delay differences between four multipath, by utilizing the difference in the same time delay difference between the pseudo source and the true position, a fuzzy plane is constructed for localization. The pseudo source can be eliminated without determining the depth relationship between the source and receiver, which can be achieved on a single hydrophone. The effectiveness of the method is verified through simulation experiments and error analysis. The sea experiment shows that the method successfully achieves distance and depth estimation of targets ranging from 11.0−16.5 km on two single hydrophones at different depths, with root mean square errors of less than 1.1 km and 54 m, respectively.
-
Keywords:
- Deep water /
- Bottom bounce area /
- Multipath delay structure /
- Distance estimation /
- Depth estimation
-
引言
深海声源定位一直是水声学领域的难点和热点问题。传统的无源定位方法为匹配场定位[1], 即利用已知的海洋环境参数仿真拷贝场, 并与实测的声信号做匹配, 20世纪末的一系列实验验证了匹配场定位在深海环境中的有效性[2-4], 但该方法易受环境失配影响。近年来, 随着深海水声物理研究的深入, 利用深海声场的各种特征进行定位的方法受到广泛关注, 形成了利用多径到达角、多径时延特征、干涉条纹特征等的一系列定位方法。其中, 多径时延是定位中的重要信息, 受到了广泛关注。
Duan等[5-6]利用海底反射波和海面海底反射波的时延差, 再结合垂直到达角信息, 实现了直达声区和海底反射区内目标的距离深度联合估计。Li等[7]提出了一种利用两类多径时延差比值的方法, 并用垂直阵处理提高增益, 实现了可靠声路径内的目标深度估计。徐嘉璘等[8]使用Randon变换提取垂直阵获得的一次海底反射6个时延差随深度的变化曲线, 实现了海底反射区声源定位。王梦圆等[9]利用直达声区内的垂直双水听器提取直达波到达时间差估计距离, 再根据直达波与海面反射波的时延差估计深度。Cao等[10]利用垂直双水听器匹配海底海面反射波和海面海底反射波的时延差, 实现了海底反射区内目标的距离深度估计。刘与涵等[11]研究了深海影区中一次海底反射声线到达垂直双水听器的时延差与距离的关系, 利用稀疏时延估计方法, 实现了近海面处垂直双水听器的距离估计。此外, 还有利用垂直到达角与频率干涉结构[12-13]与距离域幅度起伏特征[14], 匹配垂直双水听器互相关信号[15]的定位方法。
上述方法均基于垂直阵或垂直双水听器, 用单水听器或水平阵进行目标定位时, 由于没有垂直孔径, 定位难度更大。针对这种情况, Weng等[16-17]分析了直达声区和声影区深海声场的频率−距离干涉结构, 指出声强随频率存在两种干涉周期, 该干涉结构本质上是由一次海底反射多径时延差导致的, 并与收发距离和深度有关, 实验验证利用该特征, 单水听器即可实现声影区测距[18]。吴俊楠等[19]使用傅里叶变换从干涉结构中提取时延差, 实现了声影区近海面目标的测距。此外, 谢亮等[20]通过匹配多次海底反射信号的时间、幅值特征, 也实现了对声源的距离深度估计, 但实际应用中由于海底反射衰减较大, 通常只能获得经一次海底反射的信号。
已有的利用海底反射时延结构的海底反射区定位方法[8,11-19]已经总结出经一次海底反射的多径时延差中蕴含声源位置信息, 但缺少对不同收发深度下的多径时延结构的研究, 对多径时延差的利用尚不充分。例如文献[16-19]的方法仅需单水听器就能实现, 但由于都建立在接收深度大于声源深度的情况下, 通过干涉条纹结构仅使用了其中的1~2个时延差, 并认为另外2个时延差与之近似相等, 因此仅能进行距离估计而难以实现深度估计。文献[8]的方法利用了全部6条时延差, 虽然成功估计了距离和深度, 但需用垂直阵实现。本文分类讨论了接收深度大于、小于和等于声源深度情况下一次海底反射4条声线的到达结构与距离深度估计的关系; 分析了利用1~2个多径时延差定位存在的问题, 提出了一种利用4个多径时延差进行距离、深度估计的方法, 在单水听器上即可实现。通过仿真和误差分析, 并利用实验数据对该方法进行了验证。
1. 海底反射到达结构与收发深度的关系
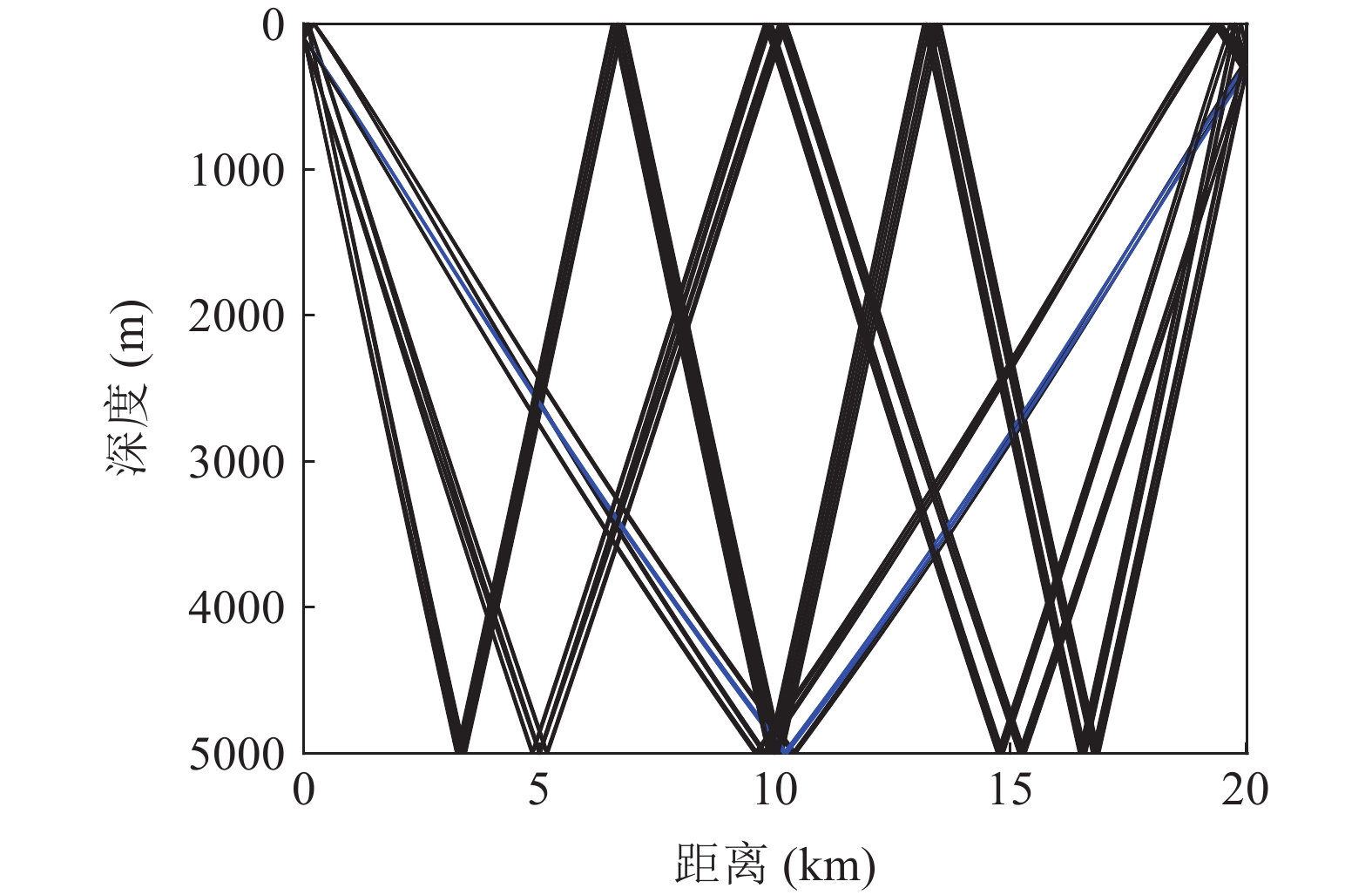
考虑典型5000 m深海声场与Munk声速剖面, 声道轴深度为1300 m, 如图1所示。海底为半无限空间, 海底声速为1550 m/s, 密度为1.7 g/cm3, 衰减系数为0.2 dB/
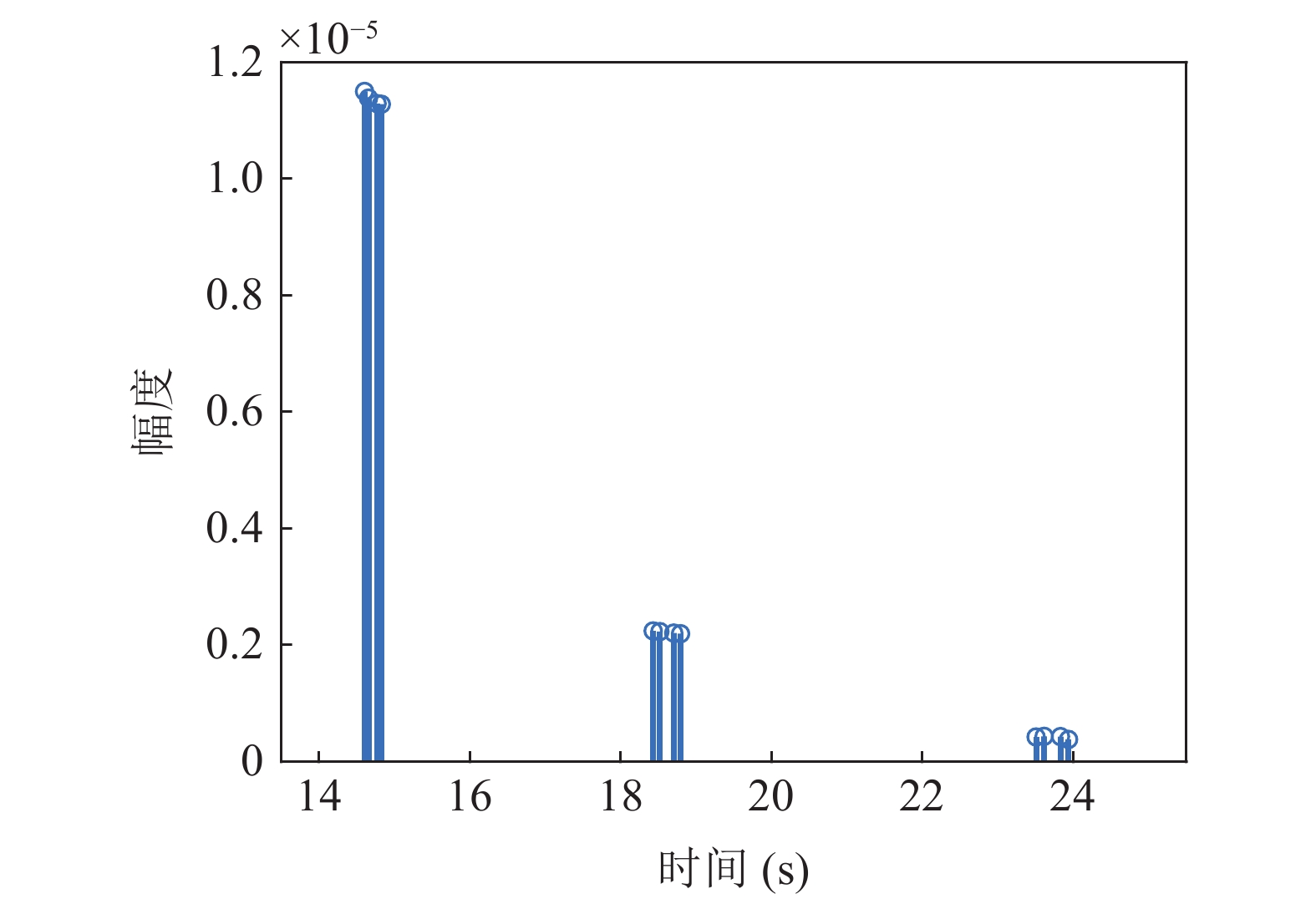
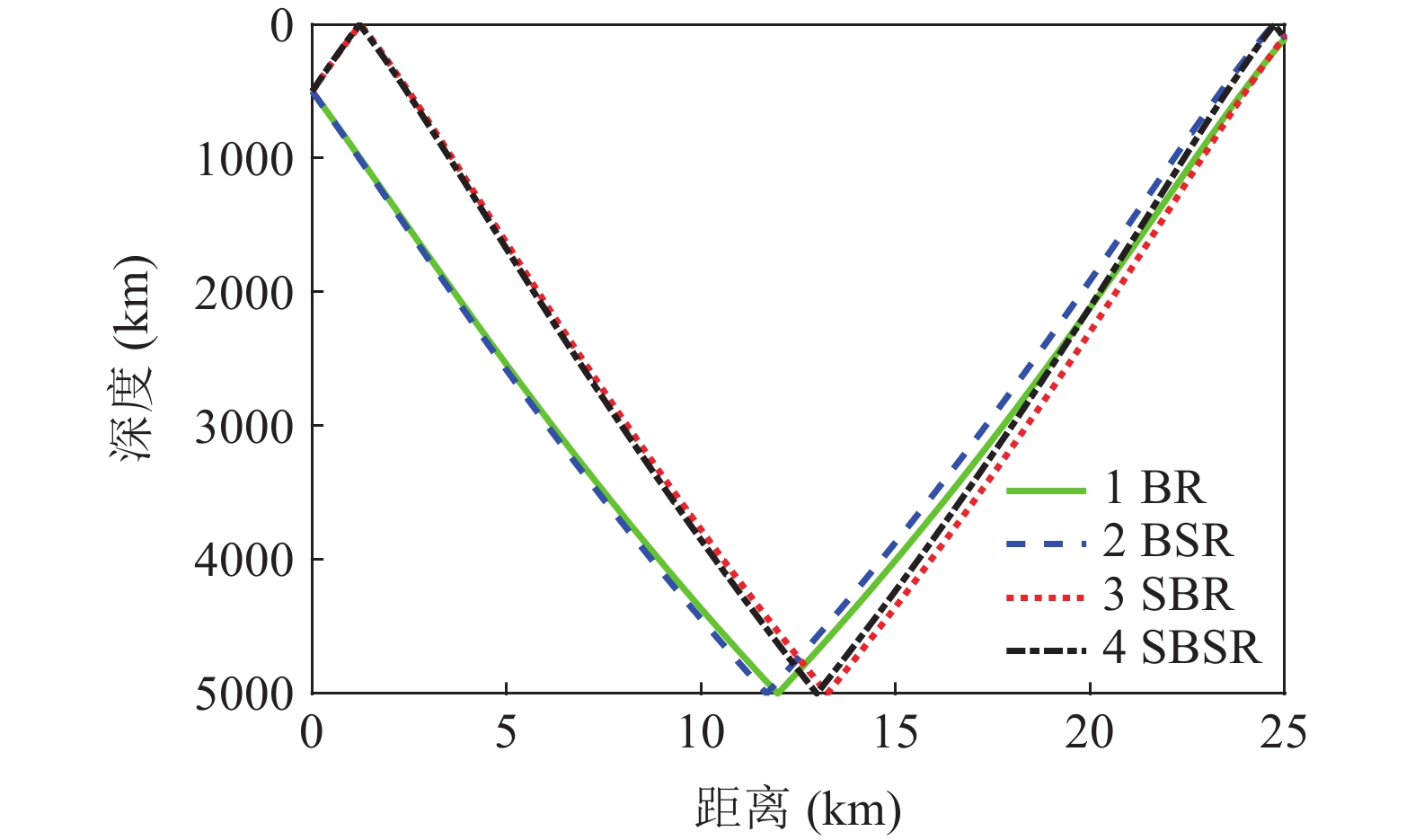
λ 。图2和图3是接收深度为300 m, 声源深度为100 m, 收发距离为20 km时海底反射声线和到达结构示意图, 频率为300 Hz。深海海底反射区中, 声场能量主要由海底反射声线提供, 由于反射损失较大, 假设二次及以上海底反射声对声场的贡献可以忽略不计, 仅考虑一次海底反射的4条声线的贡献, 分别为海底反射声线(BR)、海面−海底反射声线(SBR)、海底−海面反射声线(BSR)、海面−海底−海面反射声线(SBSR)。根据射线声学理论[21], 分层介质中声线的程函方程可以表示为水平分量和垂直分量之和:S(r,z)=S1(r)+S2(z)=rcosα0 + ∫zz0√n2(z)−cos2α0dz+C, (1) 其中,
r 表示水平距离,z 表示接收深度,α0 为出射声线俯仰角,z0 为声线起始深度,n(z)≜ 为折射率,{c_0} 为出射点声速,c\left( {\textit z} \right) 为深度{\textit z} 处的声速,C 为积分常数。本征声线传播至\left( {r,{\textit z}} \right) 处经历的时间可表示为t\left( {r,{\textit z}} \right) = \frac{1}{{{c_0}}}S\left( {r,{\textit z}} \right). (2) 在收发水平距离固定的情况下, 一次海底反射4条声线的程函水平分量相同, 而垂直分量不同, 因而产生了到达时延差。令接收深度为
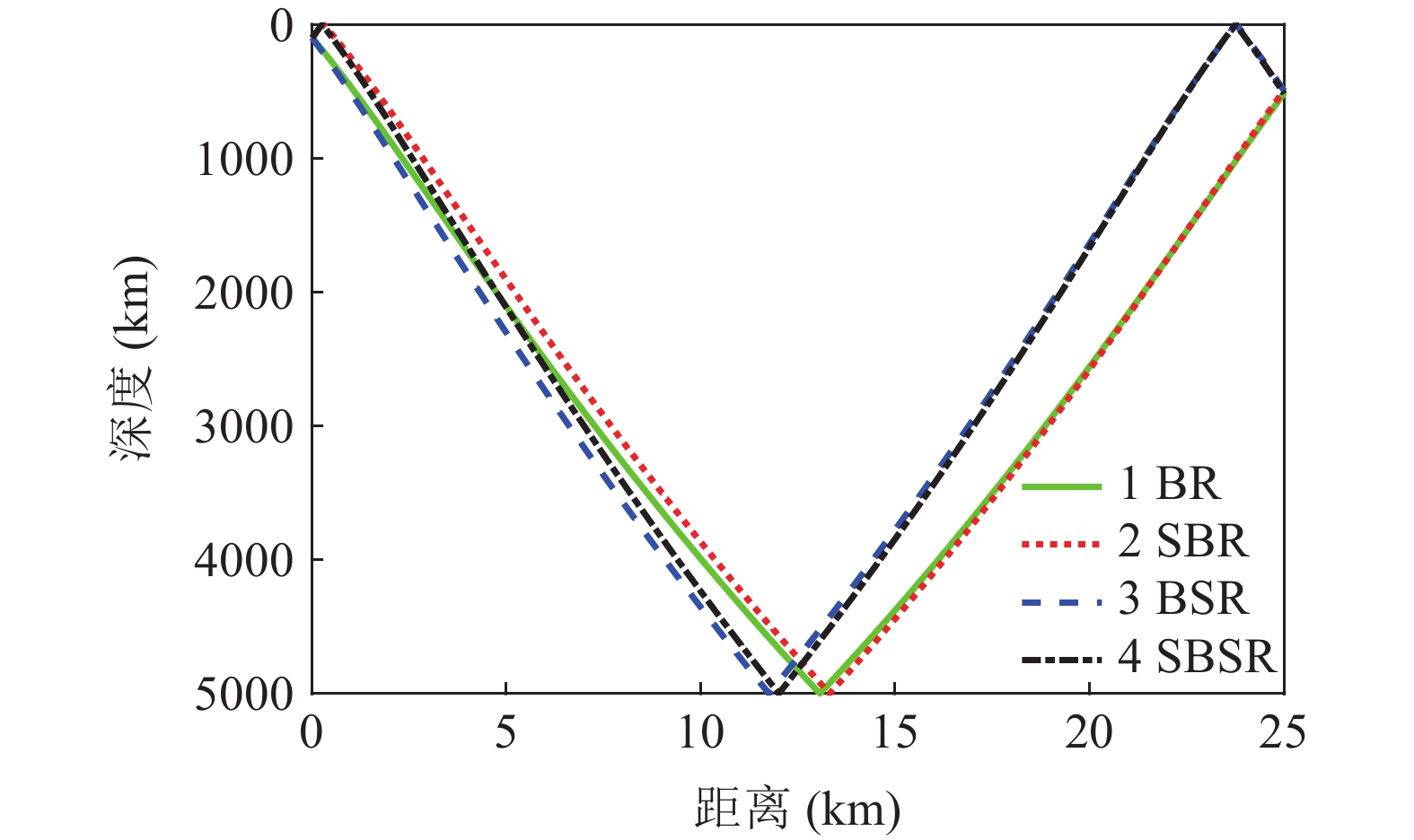
{{\textit z}_r} , 声源深度为{{\textit z}_s} , 靠近接收处的海面反射会带来2{{\textit z}_r} 的垂直分量差。由于声源出射角差别较小, 声线BSR与BR、SBSR与SBR间可以近似产生一个由接收深度决定的时延差:\left\{ \begin{gathered} {t_{{\text{BSR}}}} - {t_{{\text{BR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_r}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{BSR}}}}} {\text{d}}{\textit z},} \\ {t_{{\text{SBSR}}}} - {t_{{\text{SBR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_r}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBSR}}}}} {\text{d}}{\textit z},} \\ \end{gathered} \right. (3) 其中,
{\alpha _{{\text{BSR}}}},\;{\alpha _{{\text{SBSR}}}} 分别表示声线BSR, SBSR的出射掠射角。在理想海底条件下, 该时延差由海深、声速剖面、声源距离和接收深度决定, 与底质和频率无关[22]。因此在已知海深、声速剖面和接收深度的情况下, 通过这组时延差可以实现声源距离估计, 本文称之为距离时延差。同理, 靠近声源处的海面反射会带来
2{{\textit z}_s} 的垂直分量, 使得声线SBR与BR、SBSR与BSR间产生一个由声源深度决定的时延差:\left\{ \begin{gathered} {t_{{\text{SBR}}}} - {t_{{\text{BR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_s}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBR}}}}} {\text{d}}{\textit z},} \\ {t_{{\text{SBSR}}}} - {t_{{\text{BSR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_s}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBSR}}}}} {\text{d}}{\textit z},} \\ \end{gathered} \right. (4) 其中,
{\alpha _{{\text{SBR}}}} 表示声线SBR的出射掠射角。在理想海底条件下, 该时延差由海深、声速剖面、声源距离和声源深度决定, 与底质和频率无关[22]。因此在已知海深、声速剖面和声源距离的情况下, 通过这组时延差可以实现声源深度估计, 本文称之为深度时延差。通过这两类时延差可以实现声源的距离与深度估计, 且声源深度估计需要先进行距离估计, 因此首先关注距离时延差。然而在收发深度大小不同的情况下, 这4条声线的到达顺序不同, 对应的时延差顺序也会不同, 下面将实际可能出现的收发深度关系分为3类进行讨论。对于单水听器或水平阵接收情况, 通常接收深度是已知、可控的, 而声源深度是未知的, 因此本文中均以接收深度作为参考。
情况1: 接收深度大于发射深度。如图4所示, 此时到达接收点的声线依次为1 BR, 2 SBR, 3 BSR, 4 SBSR。到达时延差为
\left\{ \begin{gathered} \Delta {t_{{\text{2}}1}} = {t_{{\text{SBR}}}} - {t_{{\text{BR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_s}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBR}}}}} {\text{d}}{\textit z},} \\ \Delta {t_{4{\text{3}}}} = {t_{{\text{SBSR}}}} - {t_{{\text{BSR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_s}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBSR}}}}} {\text{d}}{\textit z},} \\ \end{gathered} \right. (5) \left\{ \begin{gathered} \Delta {t_{{\text{3}}1}} = {t_{{\text{BSR}}}} - {t_{{\text{BR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_r}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{BSR}}}}} {\text{d}}{\textit z},} \\ \Delta {t_{4{\text{2}}}} = {t_{{\text{SBSR}}}} - {t_{{\text{SBR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_r}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBSR}}}}} {\text{d}}{\textit z},} \\ \end{gathered} \right. (6) 其中, 时延差的下标表示到达声线的顺序, 如
\Delta {t_{21}} 表示第2条到达声线的时间减去第1条到达声线的时间的差值。由于出射掠射角近似相等, 而{{\textit z}_r} > {{\textit z}_s} , 因此有\Delta {t_{21}} \approx \Delta {t_{{\text{43}}}} < \Delta {t_{{\text{3}}1}} \approx \Delta {t_{{\text{4}}2}} 。此时距离时延差为\Delta {t_{{\text{3}}1}} ,\;\Delta {t_{{\text{42}}}} , 深度时延差为\Delta {t_{21}} ,\;\Delta {t_{{\text{43}}}} 。情况2: 接收深度小于发射深度。如图5所示, 此时到达接收点的声线依次为1 BR, 2 BSR, 3 SBR, 4 SBSR。到达时延差为
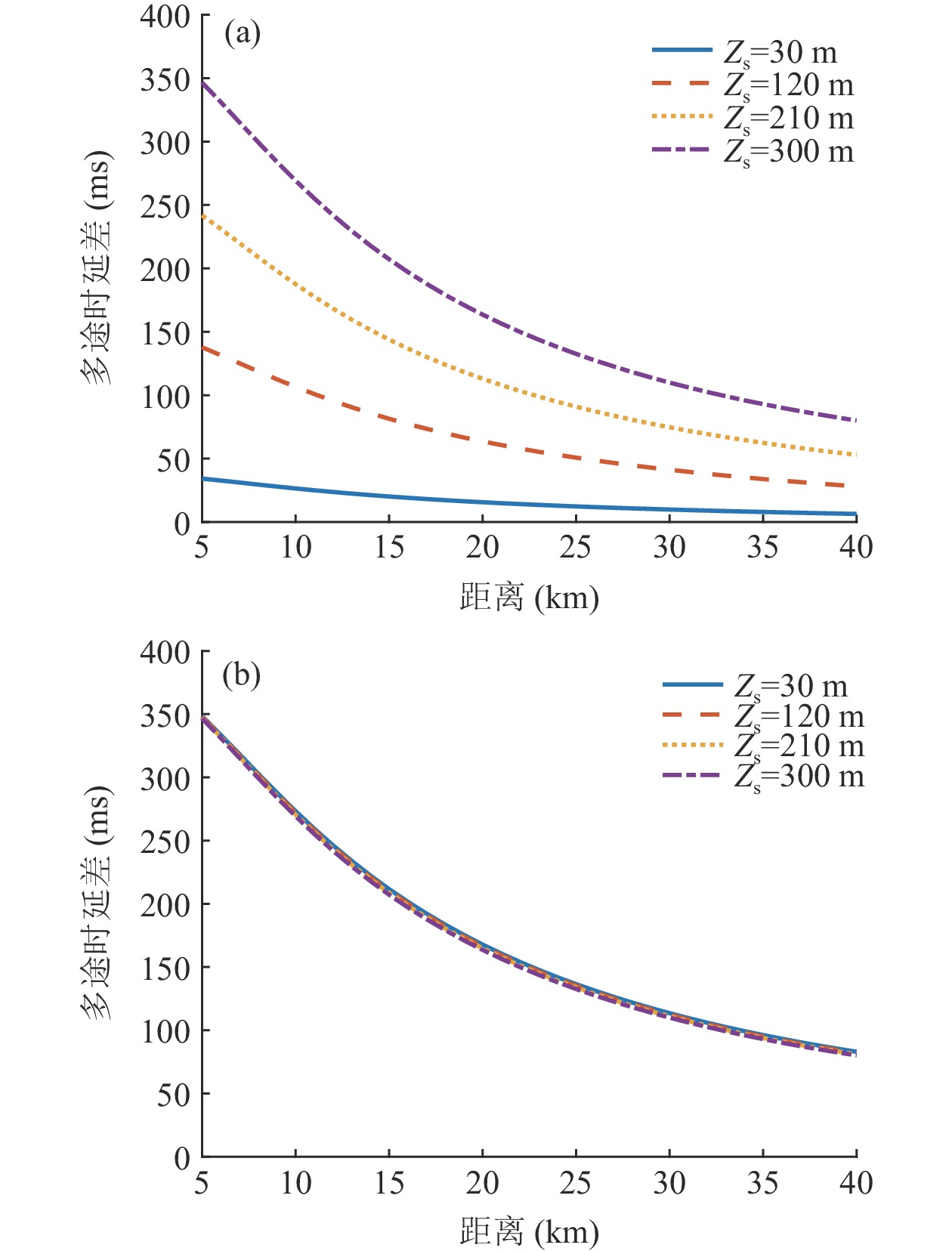
\left\{ \begin{gathered} \Delta {t_{21}} = {t_{{\text{BSR}}}} - {t_{{\text{BR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_r}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{BSR}}}}} {\text{d}}{\textit z},} \\ \Delta {t_{43}} = {t_{{\text{SBSR}}}} - {t_{{\text{SBR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_r}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBSR}}}}} {\text{d}}{\textit z},} \\ \end{gathered} \right. (7) \left\{ \begin{gathered} \Delta {t_{31}} = {t_{{\text{SBR}}}} - {t_{{\text{BR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_s}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBR}}}}} {\text{d}}{\textit z},} \\ \Delta {t_{42}} = {t_{{\text{SBSR}}}} - {t_{{\text{BSR}}}} \approx \frac{2}{{{c_0}}}\int_0^{{{\textit z}_s}} {\sqrt {{n^2}\left( {\textit z} \right) - {{\cos }^2}{\alpha _{{\text{SBSR}}}}} {\text{d}}{\textit z}.} \\ \end{gathered} \right. (8) 同理, 由于
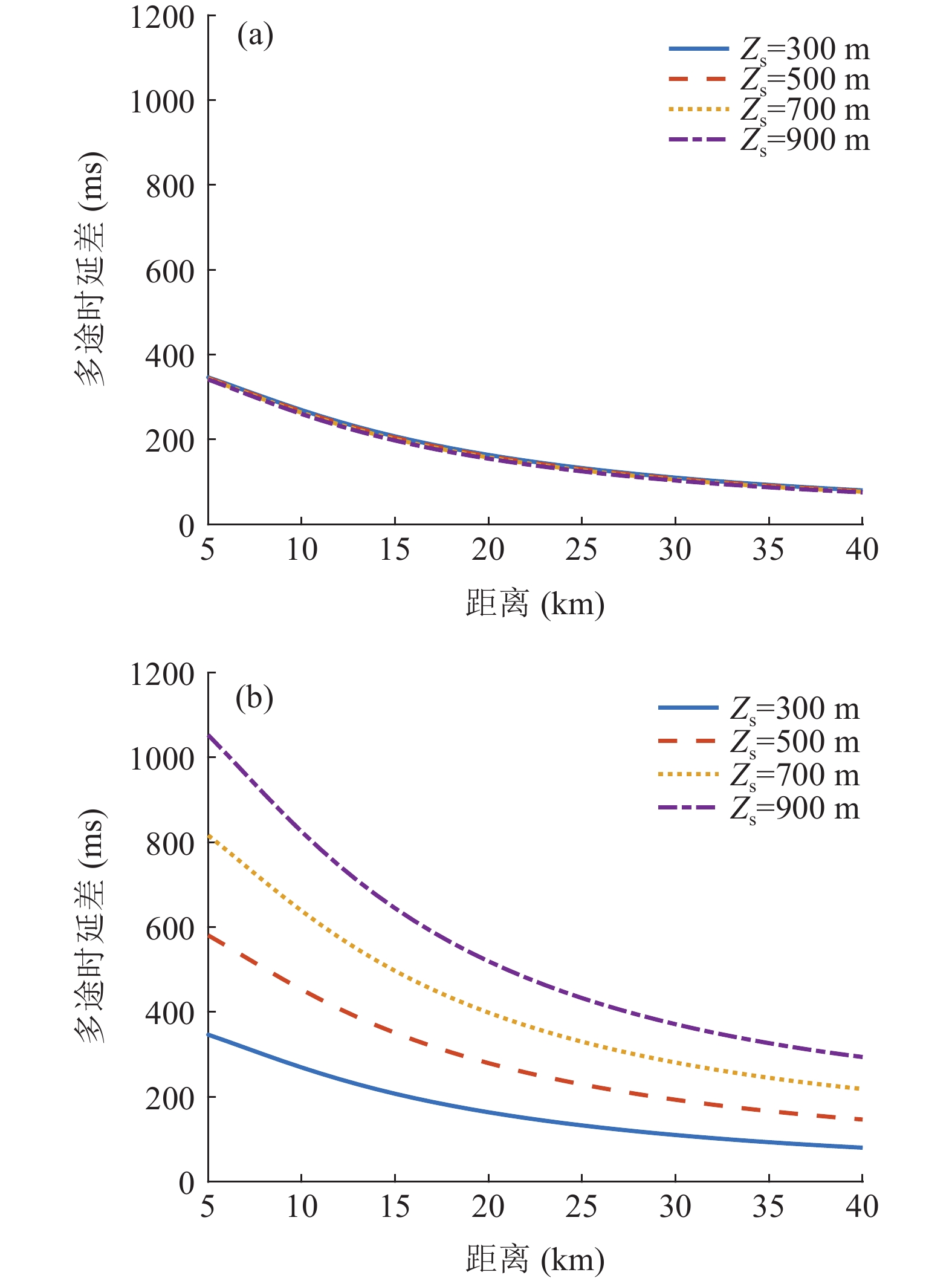
{{\textit z}_r} < {{\textit z}_s} , 同样有\Delta {t_{21}} \approx \Delta {t_{{\text{43}}}} < \Delta {t_{{\text{3}}1}} \approx \Delta {t_{{\text{4}}2}} 。此时距离时延差为\Delta {t_{21}} ,\;\Delta {t_{{\text{43}}}} , 深度时延差为\Delta {t_{{\text{3}}1}} ,\;\Delta {t_{{\text{42}}}} 。情况3: 接收深度约等于发射深度。此时第一条和最后一条到达的声线依然是BR和SBSR, 而SBR与BSR到达时间几乎相同, 即
{t_{{\text{SBR}}}} \approx {t_{{\text{BSR}}}} , 因此有\Delta {t_{21}} \approx \Delta {t_{{\text{43}}}} \approx \Delta {t_{{\text{3}}1}} \approx \Delta {t_{{\text{4}}2}} 。由于在时延结构中难以分辨SBR与BSR, 实际情况中很可能只能观察到3个到达多径, 即1 BR, 2 SBR+BSR, 3 SBSR, 其中第1, 2径间的时延差为距离时延差, 第2, 3径间的时延差为深度时延差, 且二者近似相等。综上, 收发深度的大小关系决定了到达结构与时延差的对应关系。同时, 在不考虑海底地形的情况下, 这4个多径时延差只与收发深度、声速剖面和掠射角(由声源距离和海深决定)有关, 因此可作为用于声源定位的特征。
2. 距离深度估计方法
通过第1节的分析可知, 在不同的收发深度关系下, 4条声线的到达先后不同, 使得距离、深度时延差与
\Delta {t_{21}} ,\Delta {t_{{\text{3}}1}} 的对应关系也不同。现有方法[16-19]利用从干涉条纹中提取多径时延差进行距离和深度估计, 虽然只能提取1~2个时延差, 但由于已知接收深度大于声源深度, 因此可以直接确定距离时延差、深度时延差的对应关系, 实现用1个时延差估计距离, 再结合另一个时延差估计深度。然而, 在未知收发深度关系的情况下, 仅用1~2个时延差定位存在两个问题: (1)当仅有1个时延差时, 无法确定与距离时延差的对应关系, 需要首先确定收发深度关系才能实现距离估计; (2)当有2个时延差时, 由于无法确定SBR和BSR到达的先后顺序, 可能会出现估计出两个声源位置的情况。
下面结合仿真进行说明。仿真设置与前文相同, 选取频率为300 Hz, 接收深度为300 m。如图6所示, 当
{{\textit z}_r} > {{\textit z}_s} 时,\Delta {t_{{\text{3}}1}} 是距离时延差; 如图7所示, 当{{\textit z}_r} < {{\textit z}_s} 时,\Delta {t_{21}} 是距离时延差。因此, 在未知收发深度关系时, 无法直接确定\Delta {t_{21}} ,\Delta {t_{{\text{3}}1}} 与距离、深度时延差的对应关系。为了更直观地说明多径时延差与声源位置的关系, 当接收深度等于发射深度时, 定义阈值曲线:
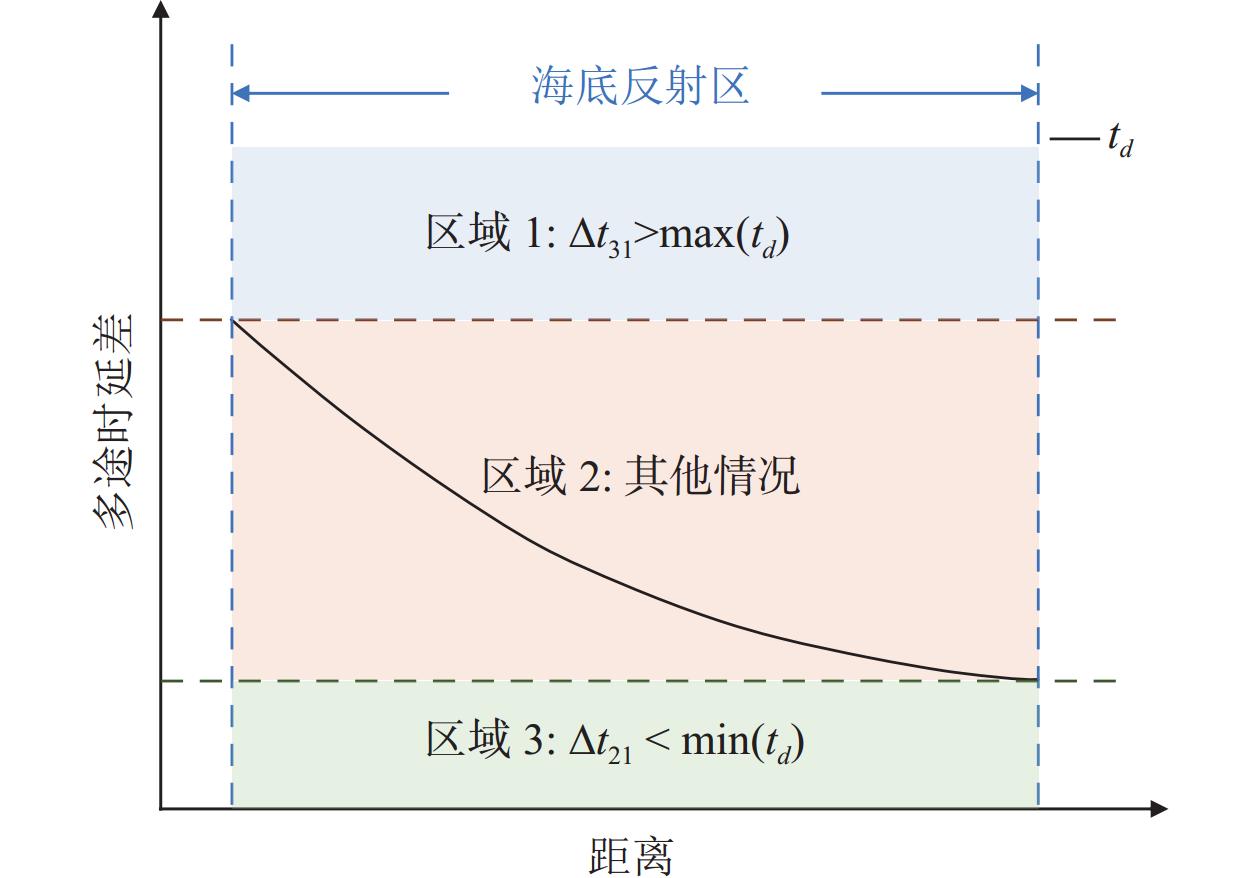
{t_d}\left( r \right) \triangleq \Delta {t_{{\text{3}}1}}\left( r \right)\left| {_{{{\textit z}_r} = {{\textit z}_s}}} \right., (9) 其中,
r 为海底反射区范围。由此可以将时延差分为3个区域进行声源深度简单判断, 如图8所示。在区域1内, 有\Delta {t_{31}} > \max \left( {{t_d}\left( r \right)} \right) , 此时{{\textit z}_r} < {{\textit z}_s} ; 在区域3内, 有\Delta {t_{21}} < \min \left( {{t_d}\left( r \right)} \right) , 此时{{\textit z}_r} > {{\textit z}_s} ; 时延差在区域2内, 此时无法直接确定收发深度关系。值得注意的是, 当声源深度位于区域1和区域3时, 由于确定了收发深度关系, 可以确定距离时延差, 从而匹配得到声源位置的唯一估计; 而在区域2内, 由于无法确定SBR与BSR到达的先后顺序, 声源会有两个可能的位置。定义模糊平面为
E\left( {r,{\textit z}} \right) = \frac{1}{{{{\left| {\Delta {t_{21}} - \Delta t_{21}^{{\text{copy}}}\left( {r,{\textit z}} \right)} \right|}^2} + {{\left| {\Delta {t_{31}} - \Delta t_{31}^{{\text{copy}}}\left( {r,{\textit z}} \right)} \right|}^2}}}, (10) 其中,
\Delta t_{21}^{{\text{copy}}}\left( {r,{\textit z}} \right) 和\Delta t_{{\text{3}}1}^{{\text{copy}}}\left( {r,{\textit z}} \right) 分别表示各位置处对应时延差的理论值, 由Bellhop程序计算。归一化模糊平面定义为
{E_N}\left( {r,{\textit z}} \right) = 10{\log _{10}}\left( {\frac{{E\left( {r,{\textit z}} \right)}}{{\max \left( {E\left( {r,{\textit z}} \right)} \right)}}} \right). (11) 仿真条件与上文相同, 接收深度
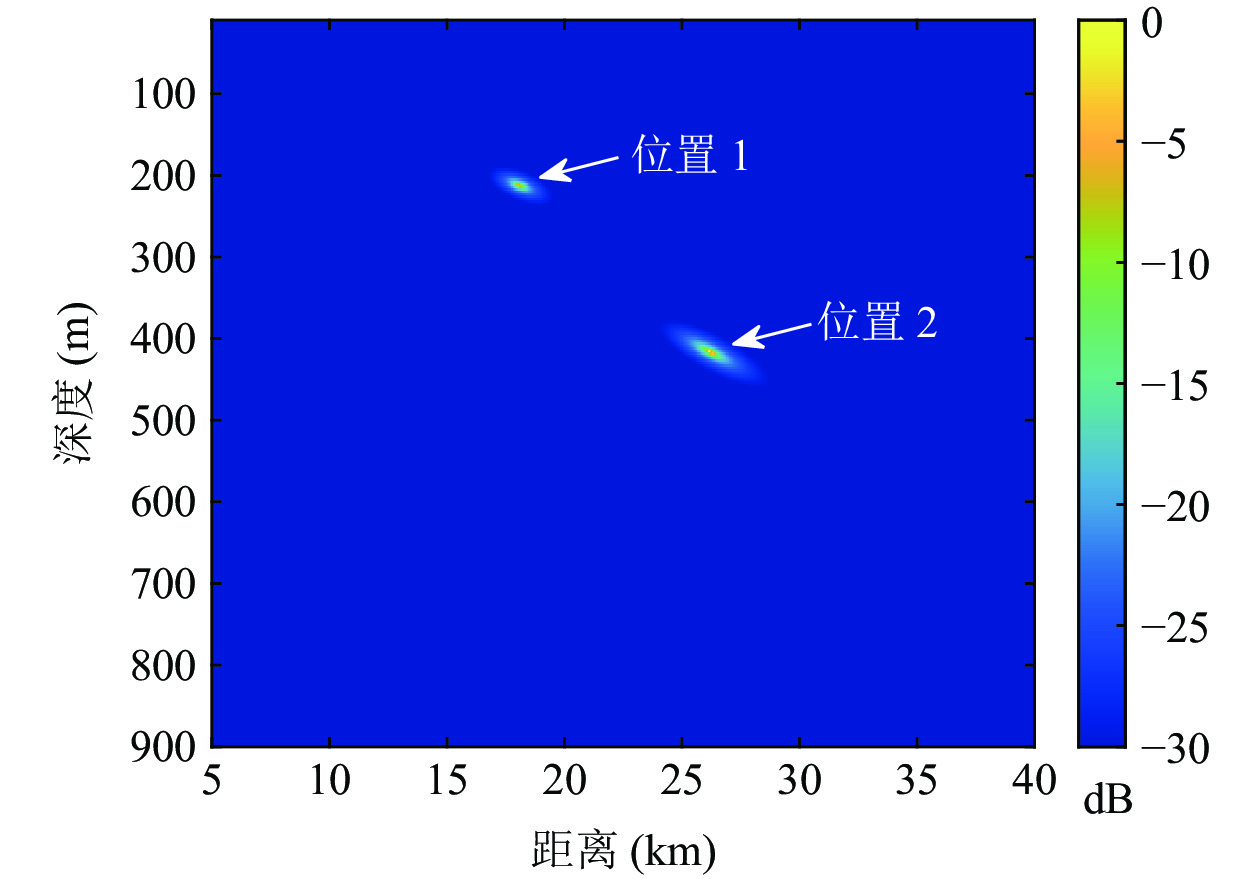
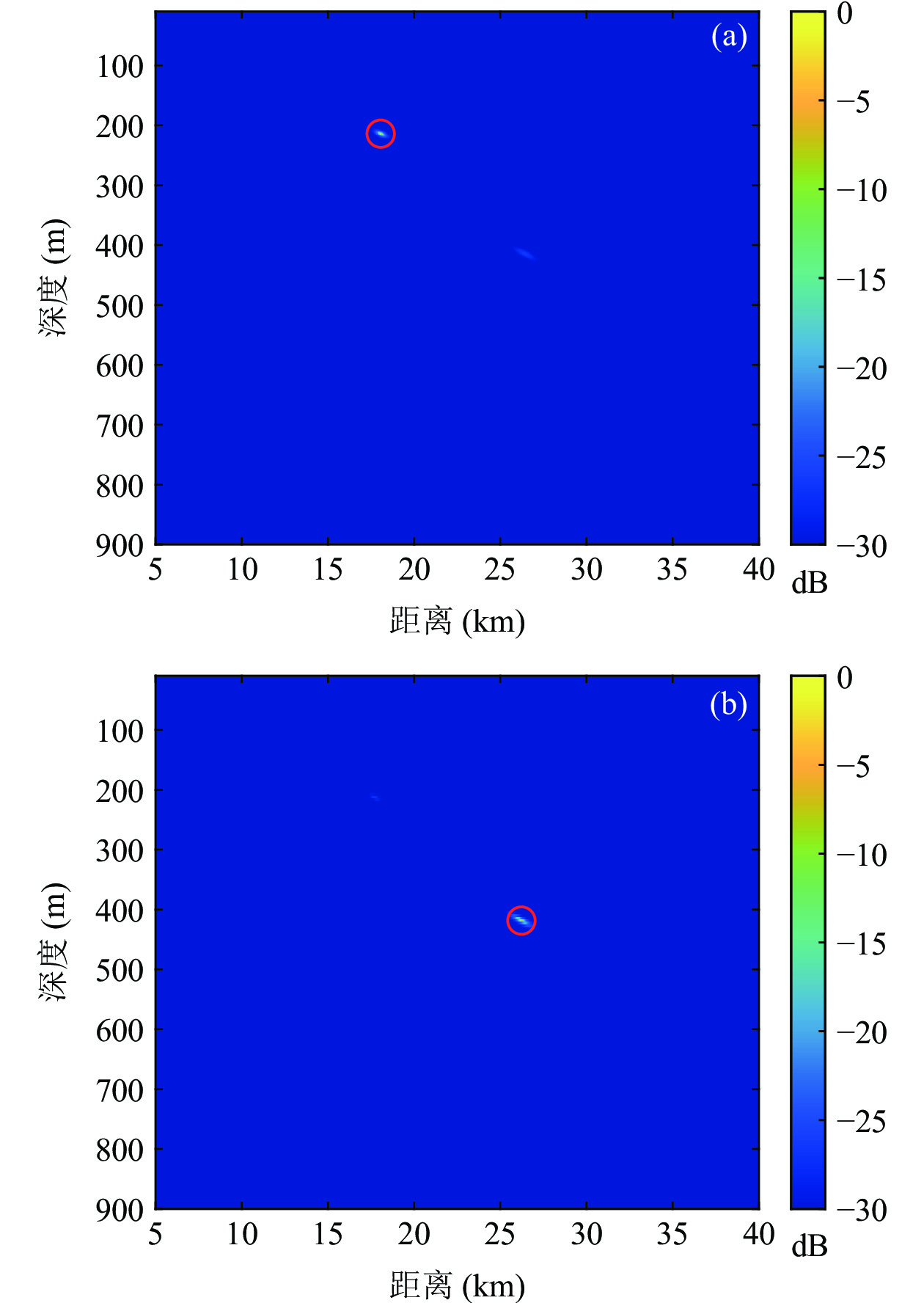
{{\textit z}_r} = 300\;{\text{m}} , 设\Delta {t_{21}} = 125\;{\text{ms}} ,\Delta {t_{{\text{3}}1}}{\text{ = 180}}\;{\text{ms}} , 此时时延差在区域2内。如图9所示, 归一化模糊平面上存在2个幅度相近的声源位置, 分别为\left( {{r_1},{{\textit z}_{s1}}} \right) = \left( {18.1\;{\text{km}},21{\text{5}}\;{\text{m}}} \right) ,\left( {{r_{\text{2}}},{{\textit z}_{s{\text{2}}}}} \right) = \left( {{\text{26}}.{\text{2}}\;{\text{km}},{\text{420}}\;{\text{m}}} \right) , 可见此时声源深度会有小于或大于接收深度两种可能。为了解决以上问题, 本文提出了利用4个时延差的距离深度估计方法, 该方法无需进行收发深度关系的判别, 通过在模糊平面上寻找峰值, 能够直接实现距离和深度估计。现有的定位方法中, 对时延差做了近似, 认为
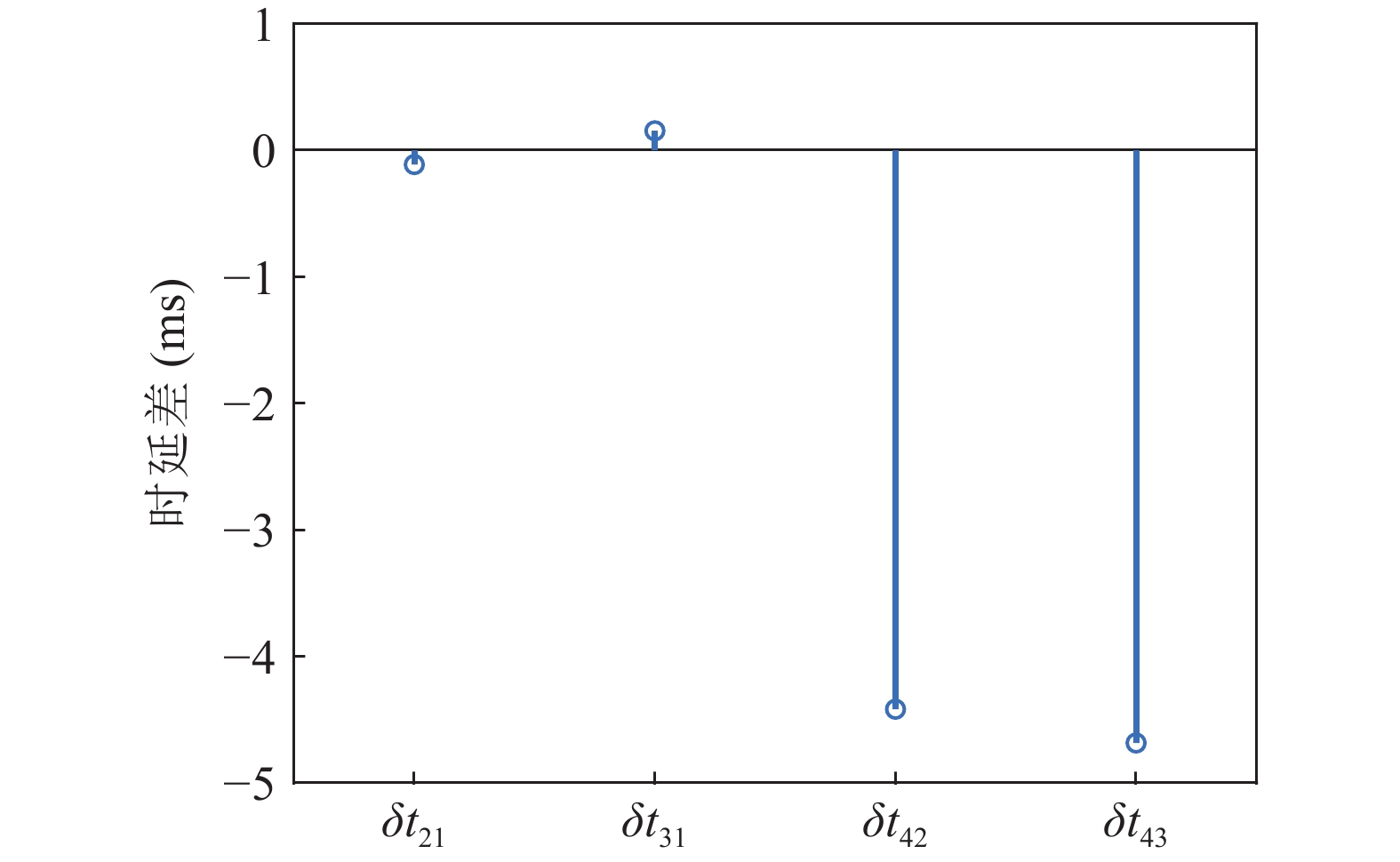
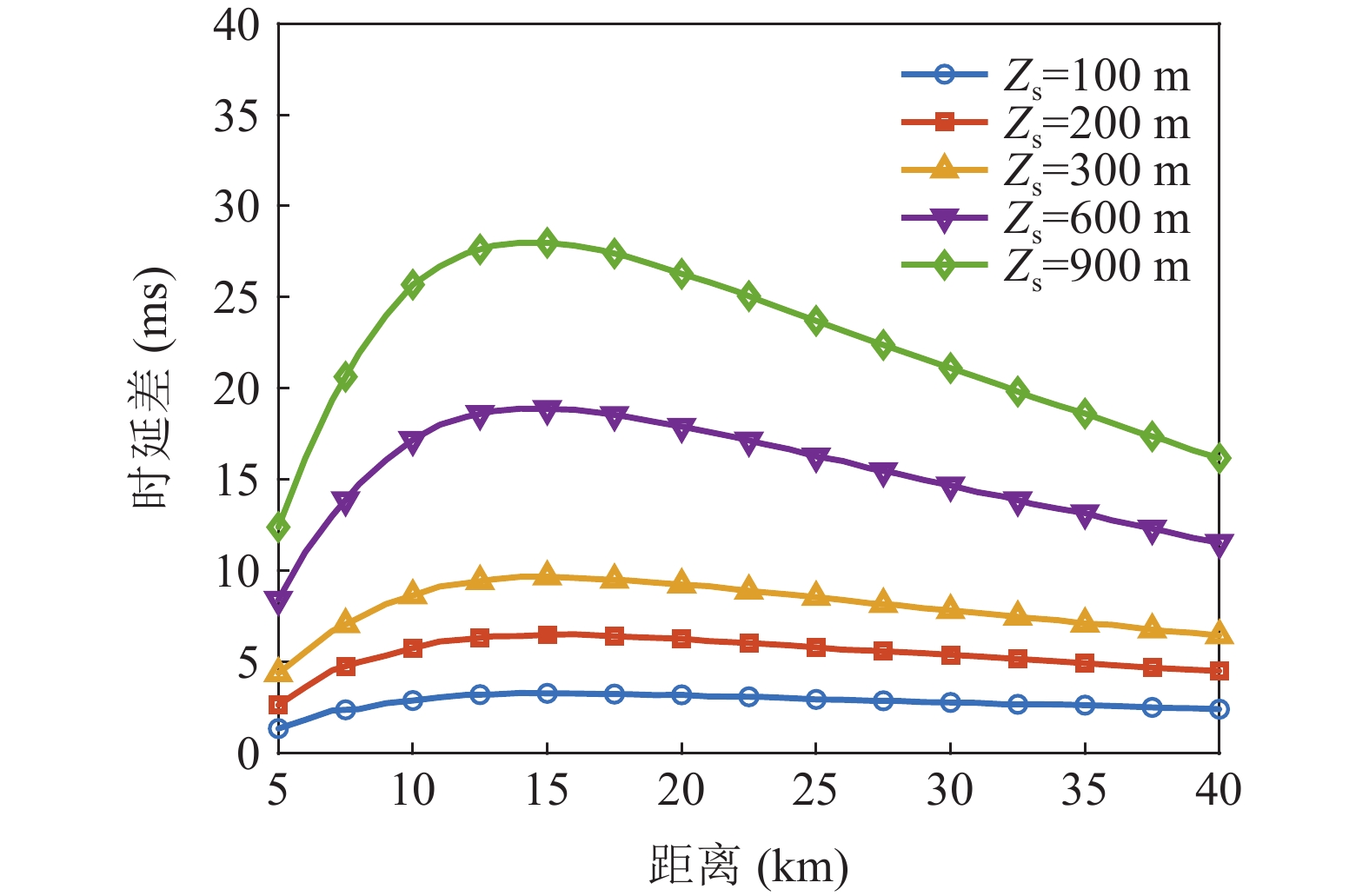
\Delta {t_{21}} \approx \Delta {t_{{\text{43}}}},\;\Delta {t_{31}} \approx \Delta {t_{{\text{42}}}} 。实际上由于垂直方向上的声程差, 4条声线的出射角有较小的区别,\Delta {t_{21}} 与\Delta {t_{{\text{43}}}} 以及\Delta {t_{31}} 与\Delta {t_{{\text{42}}}} 之间也有较小的差值。以图9中定位结果为例, 记2个位置同种时延差之差为\delta t , 例如\delta {t_{21}} = \Delta {t_{21}}\left( {{r_1},{{\textit z}_1}} \right) - \Delta {t_{21}}\left( {{r_2},{{\textit z}_2}} \right) , 如图10所示,\delta {t_{21}} 与\delta {t_{31}} 很小, 而\delta {t_{{\text{42}}}} 与\delta {t_{{\text{43}}}} 明显更大, 说明这2个位置的\Delta {t_{{\text{42}}}} 和\Delta {t_{{\text{43}}}} 有较明显的区别, 这一特征可用于进一步确定声源位置。文献[8]使用了4条多径的全部6个时延差, 实际上\Delta {t_{21}} ,\Delta {t_{{\text{3}}1}} ,\Delta {t_{{\text{4}}1}} 这3个时延差就包含了4条多径的全部时延信息, 本文为了便于理解, 使用4个时延差进行定位。图11展示了\Delta {t_{{\text{43}}}} - \Delta {t_{21}} (显然有\Delta {t_{{\text{43}}}} - \Delta {t_{21}}{\text{ = }}\Delta {t_{{\text{42}}}} - \Delta {t_{{\text{3}}1}} )与声源位置的关系, 可见这个差值随声源深度增加而增加, 且在整个海底反射区内大小可观, 在常规时延估计方法可达到的范围内。这是由于声源深度越大, 掠射角相差越大, 近似相等条件不再成立, 同理差值也随接收深度增大而增大。因此, 加入\Delta {t_{{\text{42}}}} 和\Delta {t_{{\text{43}}}} 的信息可实现海底反射区内声源的准确位置估计。定义模糊平面为
{E_{\text{4}}}\left( {r,{\textit z}} \right) = \frac{1}{{{{\left| {\Delta {t_{21}} - \Delta t_{21}^{{\text{copy}}}\left( {r,{\textit z}} \right)} \right|}^2} + {{\left| {\Delta {t_{31}} - \Delta t_{31}^{{\text{copy}}}\left( {r,{\textit z}} \right)} \right|}^2} + {{\left| {\Delta {t_{42}} - \Delta t_{42}^{{\text{copy}}}\left( {r,{\textit z}} \right)} \right|}^2} + {{\left| {\Delta {t_{43}} - \Delta t_{43}^{{\text{copy}}}\left( {r,{\textit z}} \right)} \right|}^2}}}, (12) 归一化模糊平面定义为
{E_{4N}}\left( {r,{\textit z}} \right) = 10{\log _{10}}\left( {\frac{{{E_{\text{4}}}\left( {r,{\textit z}} \right)}}{{\max \left( {{E_{\text{4}}}\left( {r,{\textit z}} \right)} \right)}}} \right). (13) 利用4个时延差对图9中的2个声源进行定位, 结果如图12所示, 声源位置处出现明显峰值, 另一位置处由于时延匹配度下降, 幅度明显降低。
3. 误差分析
在实际应用中, 测量得到的接收深度与海洋环境参数通常或多或少会有一定偏差, 本节分别讨论接收深度和海水深度的偏差对4个时延差测距测深结果的影响, 仿真环境与前文相同。
首先是接收深度。在海洋环境中, 由于风浪等因素的影响, 接收系统的深度通常会有一定的起伏, 深度传感器也会有一定的测量误差。接收深度会影响声线的俯仰角和距离时延差的积分范围, 从而影响定位结果。设置实际接收深度300 m, 声源深度100 m, 海深5000 m, 接收深度偏差在
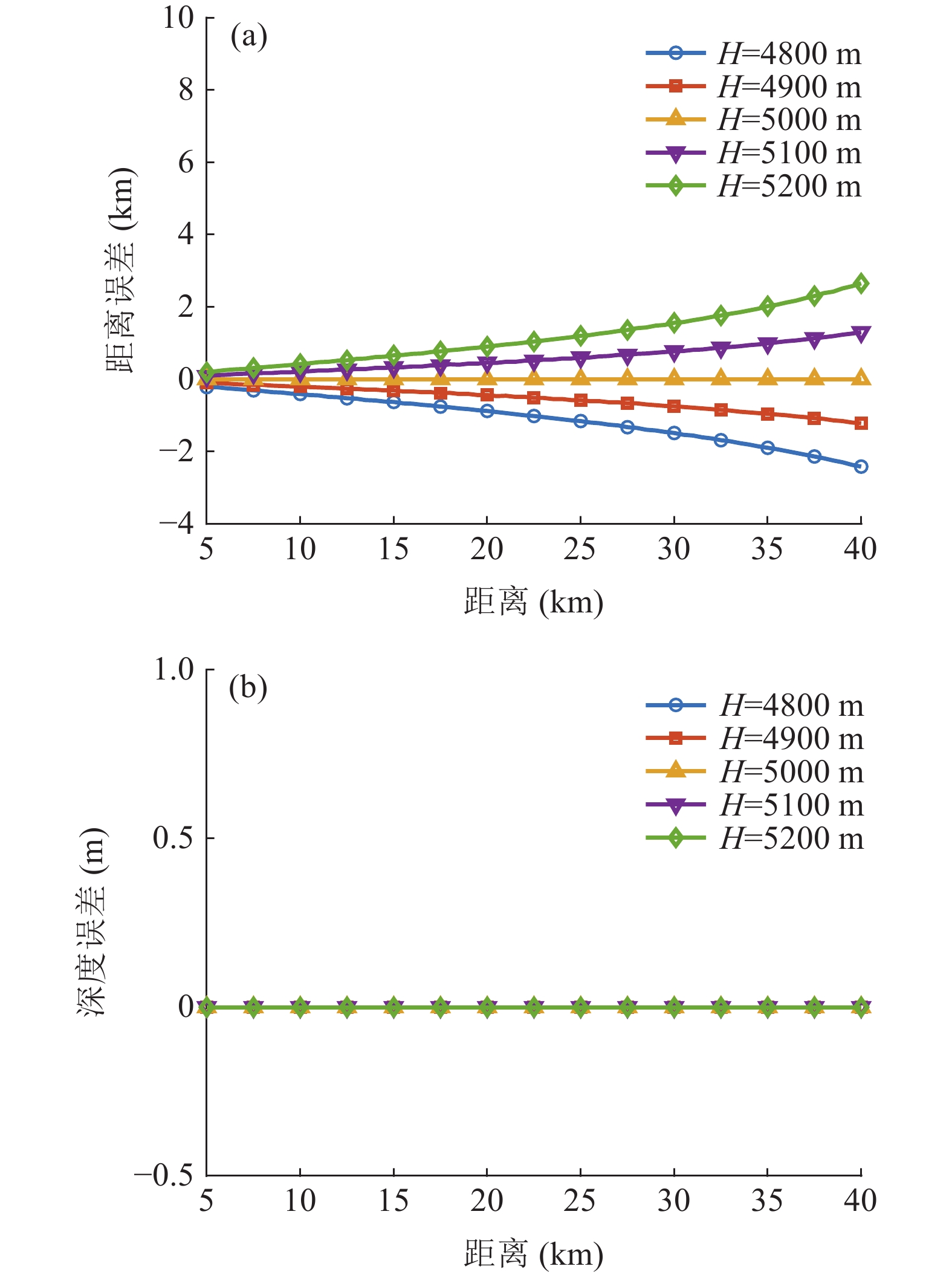
\pm 10 m,\pm 20 m时不同距离上的距离和深度估计误差如图13所示。接收深度偏差越大, 估计误差越大; 接收深度比真实值小时, 距离与深度估计值偏小, 接收深度比真实值大时, 估计值偏大; 随声源距离增加, 距离估计误差先减小再增大, 深度估计误差缓慢增加, 40 km处接收深度偏差20 m时距离估计误差约为2.9 km。其次是海水深度, 海水深度的误差会影响声线的俯仰角, 从而影响定位结果。设置接收深度300 m, 声源深度100 m, 实际海深5000 m。海水深度偏差在
\pm 100 m,\pm 200 m时不同距离上的距离和深度估计误差如图14所示。可见, 海水深度偏差越大, 距离估计误差越大, 而深度估计误差不受海水深度影响; 海水深度比真实值小时, 距离估计值偏小, 比真实值大时, 距离估计值偏大; 随声源距离增加, 距离估计误差缓慢增加, 40 km处海水深度偏差200 m时距离估计误差约为2.6 km。对比图13和图14可见, 接收深度对定位误差的影响更大, 这是由于接收深度和海水深度的改变对声线掠射角的影响有显著不同, 对到达时延产生了不同程度的影响, 进而影响了定位误差。
4. 实验验证
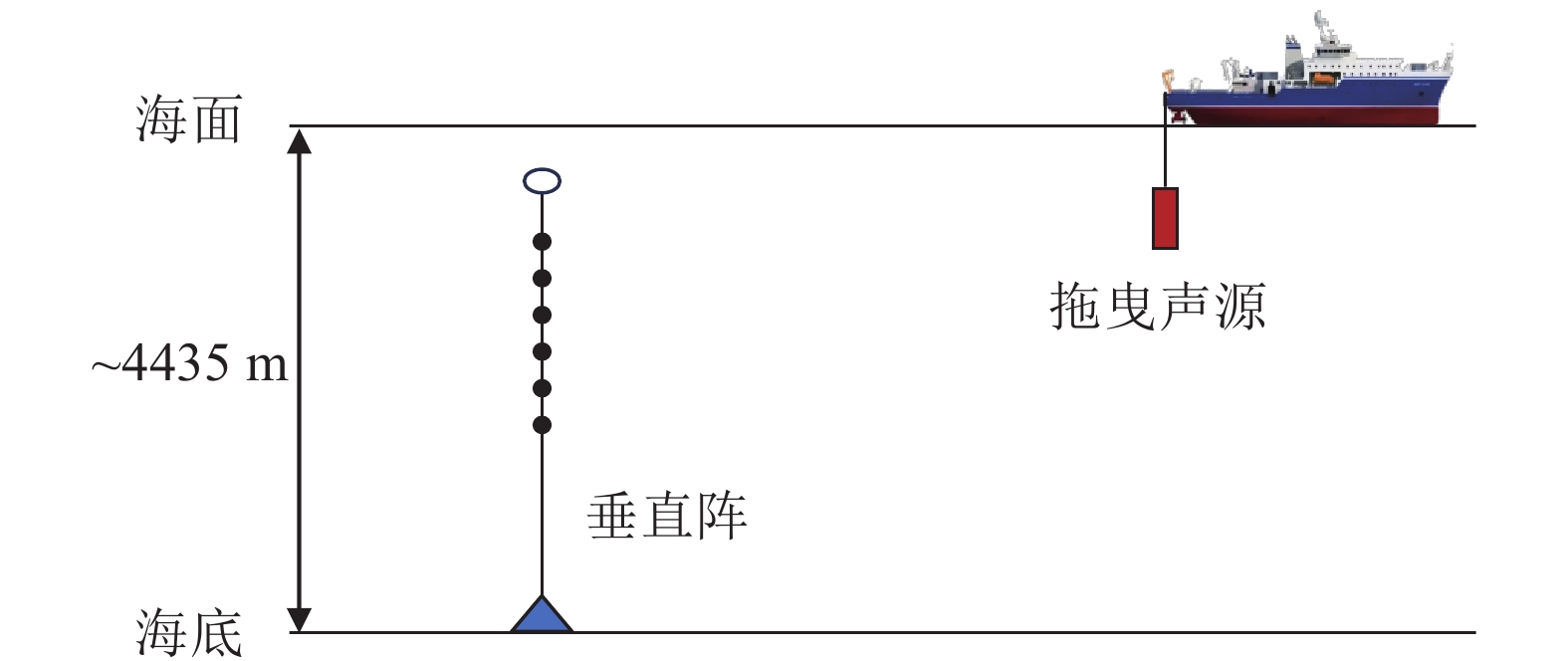
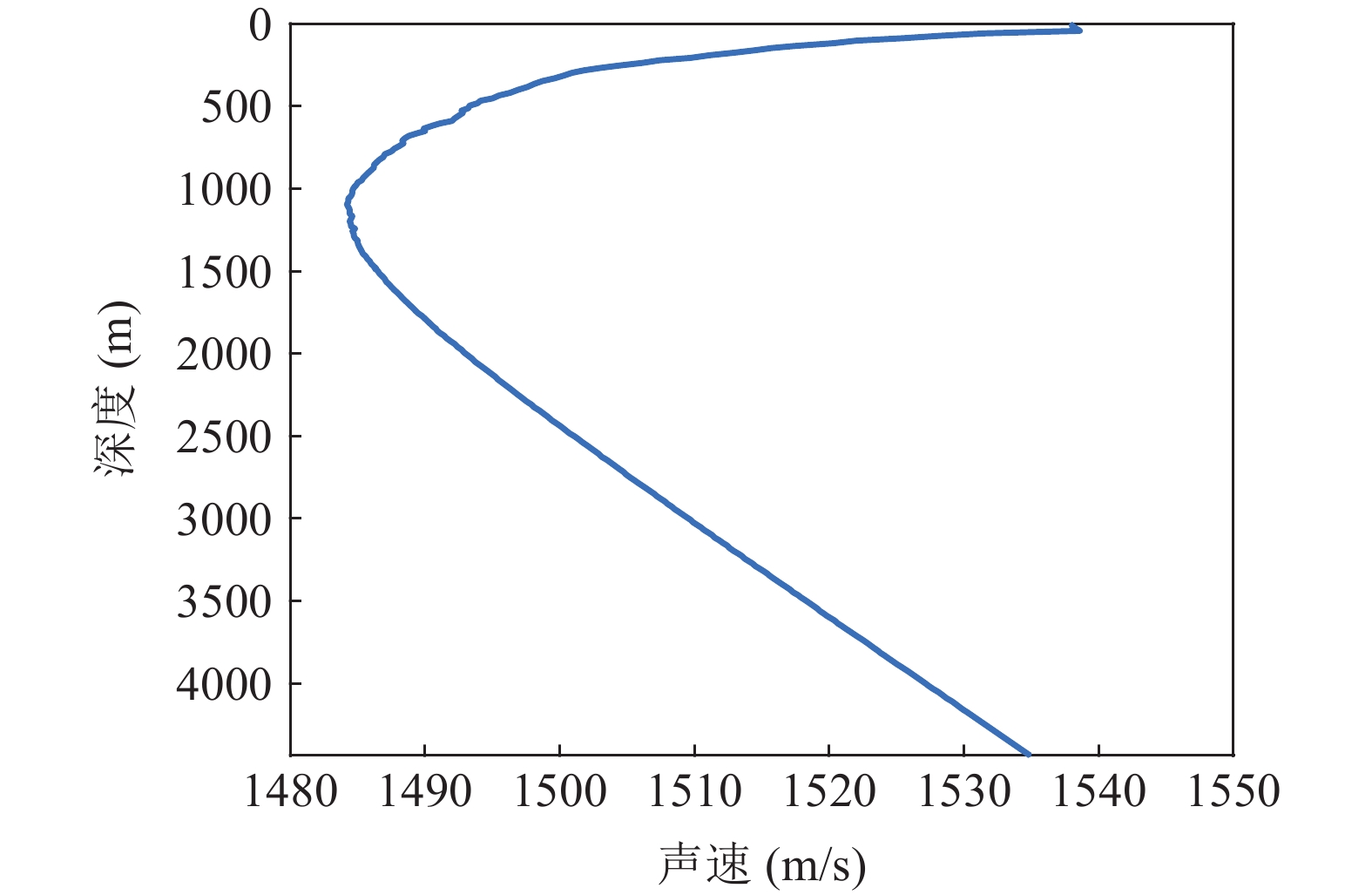
在某海域开展了一次深海声学实验, 实验地点海深约为4435 m, 实验布设情况如图15所示, 声速剖面如图16所示。实验过程中, 实验船携带声源发射LFM信号, 期间改变声源深度, 接收站点布放有自容式水听器组成的垂直阵, 取布放深度为131 m和454 m的两个水听器接收数据验证本文方法。
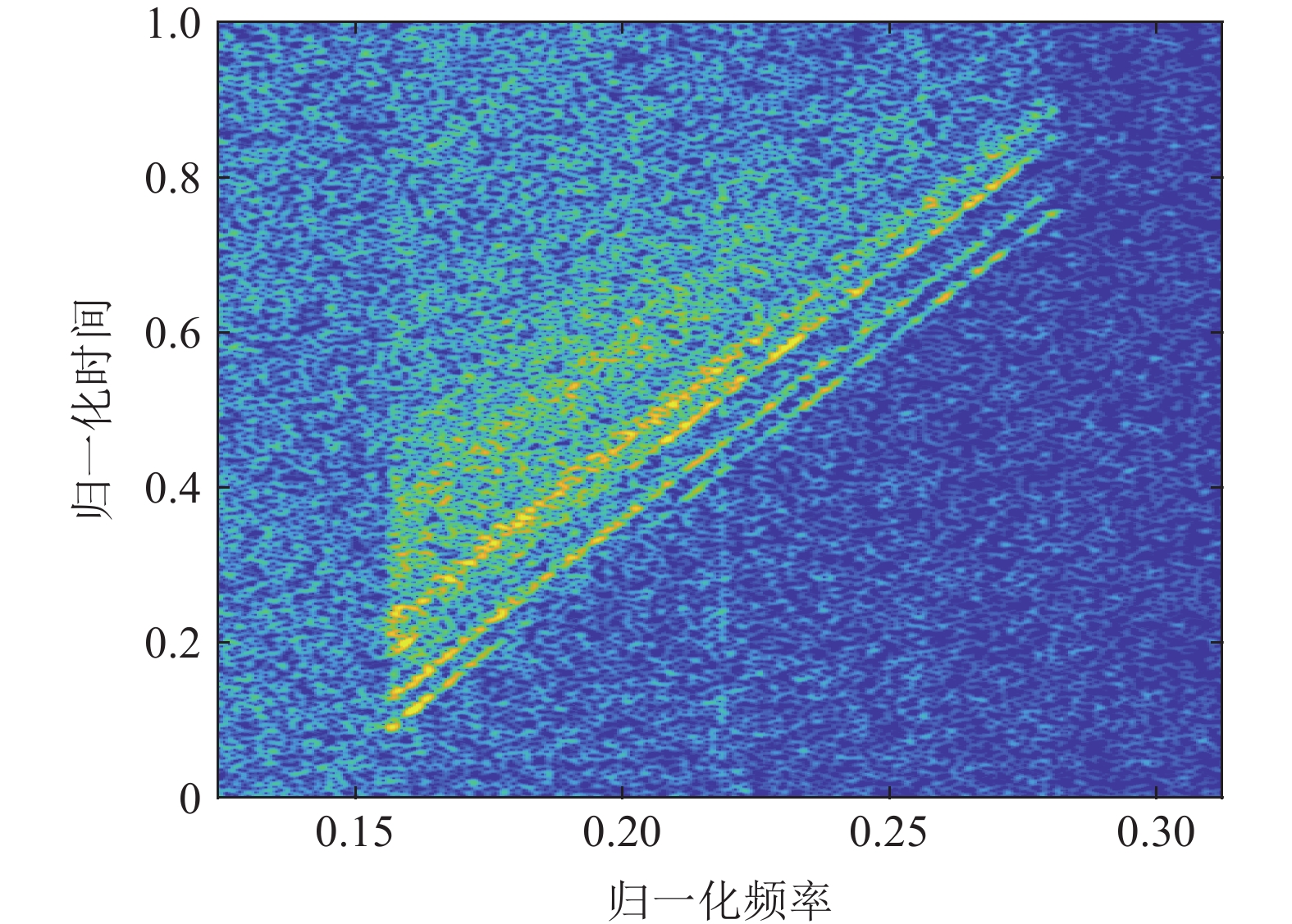
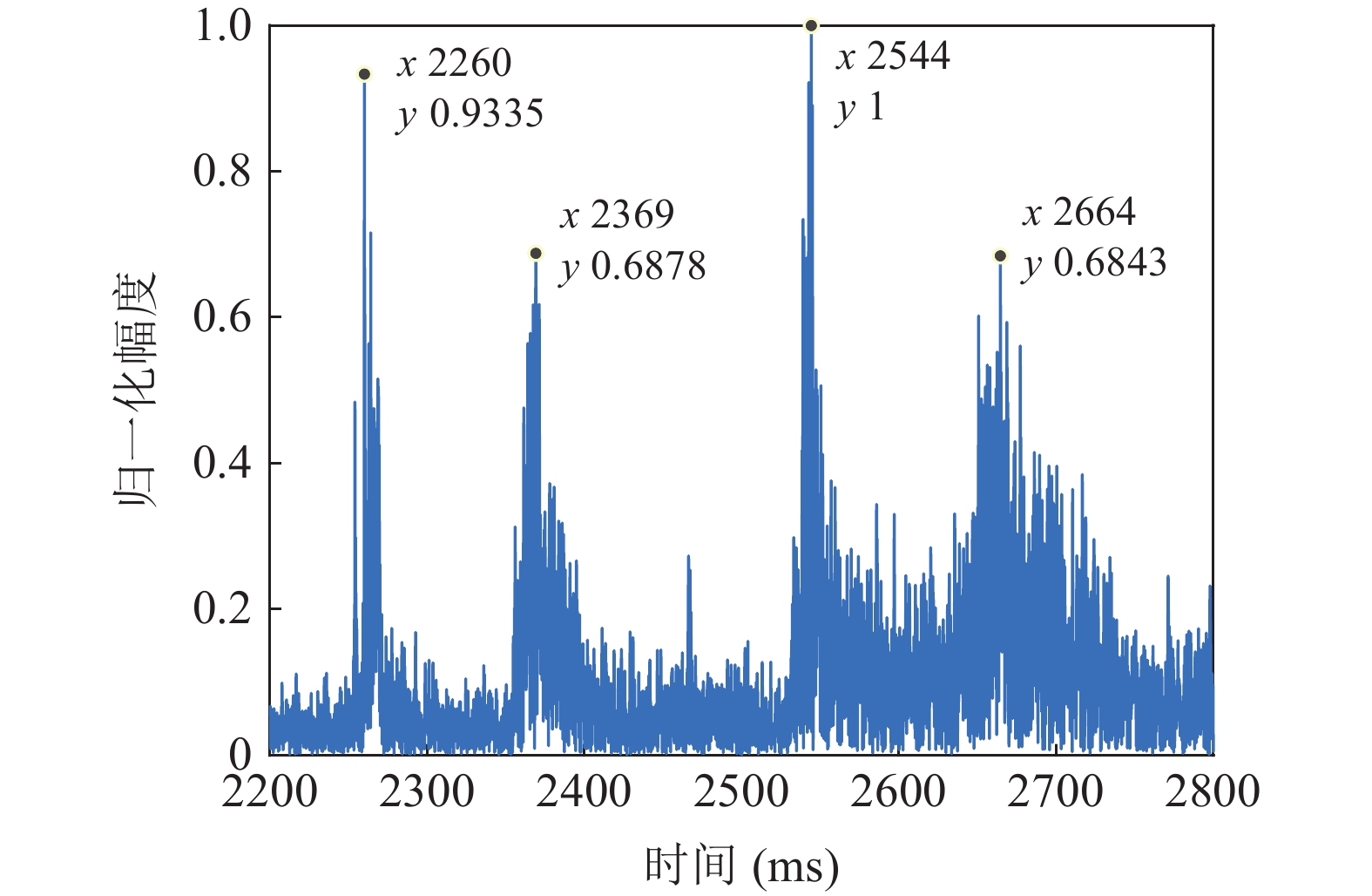
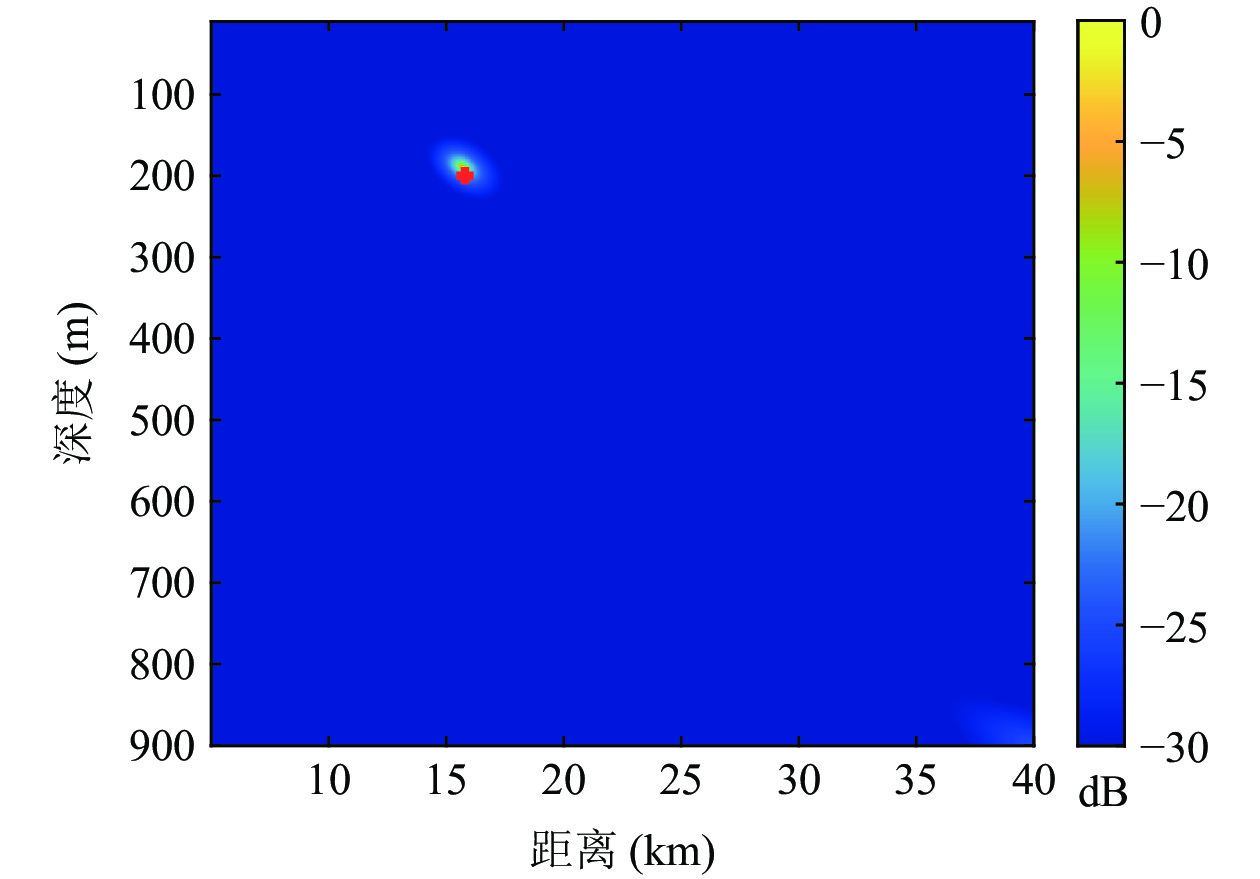
图17是深度为454 m处水听器接收到的一次海底反射信号的时频图, 声源距离为15.8 km, 声源深度为200 m。从图中可以看到明显的4个多径信号, 对接收信号进行匹配滤波的结果如图18所示, 从中提取时延差并代入模糊平面计算, 进行距离和深度估计, 归一化模糊平面如图19所示, 估计距离15.7 km, 深度189 m。
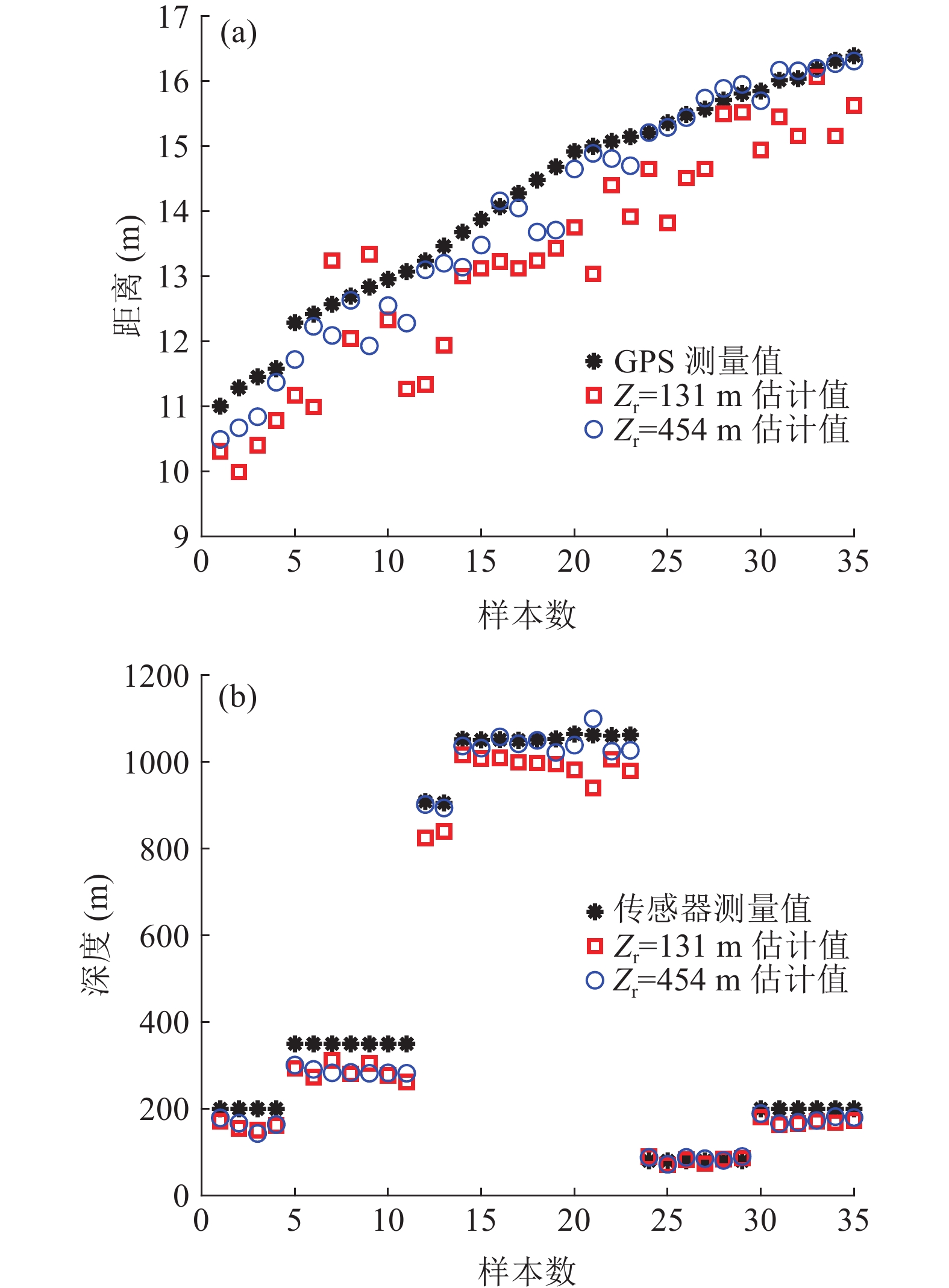
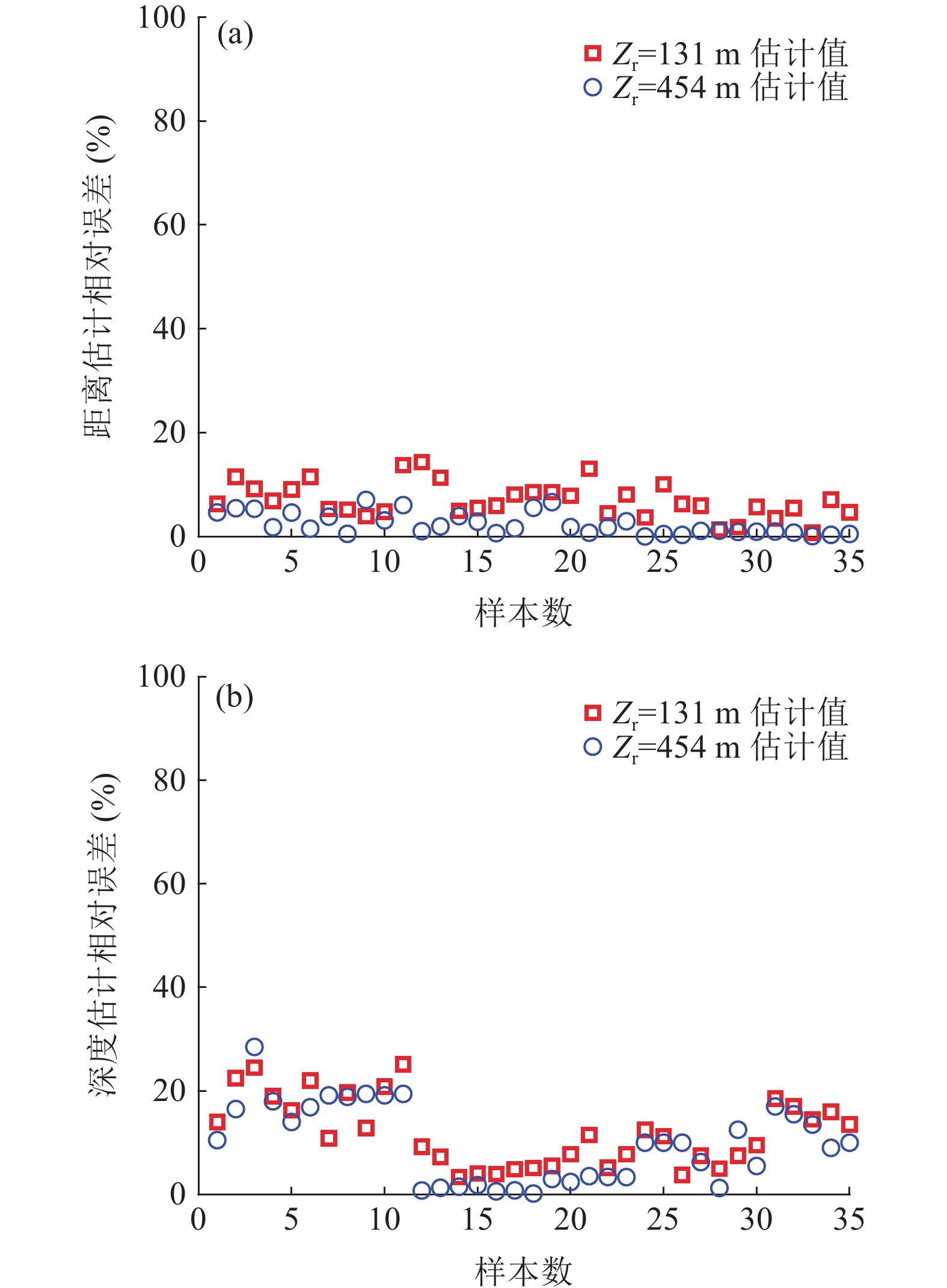
图20是不同距离和声源深度下的定位结果, 相对误差如图21所示。可见, 该方法对距离11~17 km、深度80~1100 m内的声源成功实现了定位。定位均方根误差如表1所示, 可见深度为454 m的水听器的距离和深度估计结果更好, 两个水听器的距离估计误差的均值分别为7.0%和2.4%, 深度估计误差的均值分别为12.0%和9.8%。结合第2节的理论分析可知, 这是由于对于同一位置的声源, 接收深度越深, 一方面多径到达间隔越大, 更易分辨多径时延, 对时延估计误差的鲁棒性也更强; 另一方面,
\Delta {t_{21}} 与\Delta {t_{{\text{43}}}} 、\Delta {t_{31}} 与\Delta {t_{{\text{42}}}} 的差异越大, 在模糊平面中更易区分。因此, 在利用一次海底反射多径时延差进行定位时, 适当增加接收深度, 能够提高定位精度。其次, 图20的结果显示, 两个接收深度下距离和深度估计均偏小, 根据第3节的分析, 这可能是传感器深度记录值小于实际深度, 以及测量海深小于实际海深导致的。表 1 定位均方根误差接收深度{{\textit z}_{\text{r}}}(m) 距离均方根误差 (km) 深度均方根误差 (m) 131 1.06 53.4 454 0.41 35.9 5. 结论
本文深入分析了深海海底反射区多径时延差与目标位置的关系, 解释了现有定位方法可能会估计出伪源的原因。在不同的收发深度关系下, 声线到达结构不同, 距离和深度时延差的对应关系也会发生改变。在仅有1个时延差的情况下, 需要先确定收发深度关系才能进行距离估计; 在有2个时延差的情况下, 当无法确定收发深度关系时, 可能会出现估计出两个声源位置的情况。
针对这一问题, 本文提出了一种在单水听器上利用多径时延差估计声源距离和深度的方法。所提方法通过利用完整的4个多径时延差, 无需进行收发深度关系的判别, 就能直接实现声源距离和深度估计。误差分析表明, 接收深度偏差对定位误差的影响较大; 海水深度偏差会对距离估计产生误差, 但对深度估计没有影响。实验用两个不同深度的水听器进行验证, 结果表明, 该方法成功定位了深度80~1060 m的目标, 且实验中接收深度较深的水听器定位误差更小, 这对深海探测器的布放深度有一定参考价值。
-
表 1 定位均方根误差
接收深度{{\textit z}_{\text{r}}}(m) 距离均方根误差 (km) 深度均方根误差 (m) 131 1.06 53.4 454 0.41 35.9 -
[1] Bucker H P. Use of calculated sound fields and matched-field detection to locate sound sources in shallow water. J. Acoust. Soc. Am., 1976; 59(2): 368−373 DOI: 10.1121/1.380872
[2] Tran J M Q D, Hodgkiss W S. Matched-field processing of 200-Hz continuous wave (cw) signals. J. Acoust. Soc. Am., 1991; 89(2): 745−755 DOI: 10.1121/1.1894634
[3] Westwood E K. Broadband matched-field source localization. J. Acoust. Soc. Am., 1992; 91(5): 2777−2789 DOI: 10.1121/1.402958
[4] Tran J M Q D, Hodgkiss W S. Experimental observation of temporal fluctuations at the output of the conventional matched-field processor. J. Acoust. Soc. Am., 1991; 89(5): 2291−2302 DOI: 10.1121/1.400920
[5] Duan R, Yang K D, Ma Y L, et al. A reliable acoustic path: Physical properties and a source localization method. Chin. Phys. B, 2012; 21(12): 124301 DOI: 10.1088/1674-1056/21/12/124301
[6] Duan R, Yang K D, Ma Y L. Narrowband source localisation in the deep ocean using a near-surface array. Acoust. Aust., 2014; 42(1): 36−42
[7] Li H, Xu Z, Yang K, et al. Use of multipath time-delay ratio for source depth estimation with a vertical line array in deep water. J. Acoust. Soc. Am., 2021; 149(1): 524−539 DOI: 10.1121/10.0003364
[8] 徐嘉璘, 郭良浩, 任云. 深海海底声反射区多途时延差分析与近海面声源定位. 声学学报, 2023; 48(4): 618−631 DOI: 10.15949/j.cnki.0371-0025.2023.04.013 [9] 王梦圆, 李整林, 秦继兴, 等. 深海直达声区水下声源距离深度联合估计. 信号处理, 2019; 35(9): 1535−1543 DOI: 10.16798/j.issn.1003-0530.2019.09.011 [10] Cao R, Yang K, Ma Y, et al. Source localization using multi-path time delays measured by two hydrophones in the deep ocean. Acoust. Aust., 2019; 105(1): 248−252 DOI: 10.3813/AAA.919306
[11] 刘与涵, 董金鑫, 郭良浩, 等. 深海声影区稀疏时延估计与声源测距. 声学学报, 2022; 47(4): 417−431 DOI: 10.15949/j.cnki.0371-0025.2022.04.007 [12] 王文博, 苏林, 王臻, 等. 利用宽带声场频率−掠射角干涉结构的深海直达声区目标深度估计方法. 声学学报, 2021; 46(2): 161−170 DOI: 10.15949/j.cnki.0371-0025.2021.02.001 [13] 徐嘉璘, 郭良浩, 闫超. 利用深海海底声反射区频域干涉结构的声源深度估计方法. 声学学报, 2023; 48(3): 425−436 DOI: 10.15949/j.cnki.0371-0025.2023.03.001 [14] 朱启轩, 孙超, 刘雄厚. 利用海底弹射区角度−距离干涉结构特征实现声源深度估计. 物理学报, 2022; 71(18): 154−163 DOI: 10.7498/aps.71.20220746 [15] Lei Z, Yang K, Ma Y. Passive localization in the deep ocean based on cross-correlation function matching. J. Acoust. Soc. Am., 2016; 139(6): EL196−EL201 DOI: 10.1121/1.4954053
[16] 翁晋宝, 李风华, 郭永刚. 典型深海声场频率−距离干涉结构分析及实验研究. 声学学报, 2016; 41(3): 330−342 DOI: 10.15949/j.cnki.0371-0025.2016.03.008 [17] Weng J B, Yang Y M. Experimental demonstration of shadow zone localization using deep water interference patterns measured by a single hydrophone. IEEE J. Oceanic Eng., 2017; 43(4): 1171−1178 DOI: 10.1109/JOE.2017.2759698
[18] 翁晋宝, 杨燕明. 深海中利用单水听器的影区声源无源测距测深方法. 声学学报, 2018; 43(6): 905−914 DOI: 10.15949/j.cnki.0371-0025.2018.06.004 [19] 吴俊楠, 周士弘, 张岩. 利用深海海底反射声场特征的水面声源被动测距. 中国科学: 物理学 力学 天文学, 2016; 46(9): 82−88 DOI: 10.1360/SSPMA2016-00082 [20] 谢亮, 王鲁军, 林旺生. 深海脉冲信号簇到达结构特征及其在水下声源定位中的应用. 声学学报, 2021; 46(2): 171−181 DOI: 10.15949/j.cnki.0371-0025.2021.02.002 [21] 汪德昭, 尚尔昌. 水声学. 第2版. 北京: 科学出版社, 2013: 98−106 [22] 吴俊楠. 深海水平阵接收声信号场特征研究及其应用. 博士学位论文, 北京: 中国科学院声学研究所, 2017: 53−55 -
期刊类型引用(1)
1. 刘与涵,郭良浩,董阁,章伟裕,徐嘉璘,徐鹏,刘建军,任岁玲,屈嵩岳. 深海移动水平阵声源被动定位方法研究进展. 应用声学. 2025(01): 36-54 .  百度学术
百度学术
其他类型引用(0)



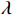
 下载:
下载: